fisicoquimica
objetivo: Dar a conocer como se relaciona la fisicoquimica, para conocer como esta compuesta cada uno de los temas que nos lleva a solucionar problemas para así poder ver cada resultado de cada tema que se presente en esta semestre
a) ¿que se va hacer?
vamos a ver como podemos solucionar los problemas que tenemos y dar a conocer como se va a realizar
b) ¿como se va hacer?
se va a realizar por medios de unos ejercicios y poder solucionarlos
c) ¿para que se va hacer?
para poder demostrar cada uno de los temas que estuvimos realizando en este semestre
introducción:
Energía: la energia es la capacidad que posee los cuerpos para poder efectuar un trabajo a causa de su constitucion energia interna,de su posicion energia potencial o de su movimiento energia cinetica.es una magnitud homogenea con el gtrabajo po lo que se mide en las mismas unidades, es decir en julio en el sistemas internacional. segun la forma o el sistema fisico en que se manifiesta, se considera diferentes formas de energía: térmica, mecánica, eléctrica, química, electromagnético, nuclear, luminosa.

Entalpia:
es la cantidad de energia de un sistema termodinamica, que este puede intercambiar con su entorno
*es una reacion química a presión constante, rl cambio de entalpia del sistemos es el calor absorbido o desprendido en la reacion

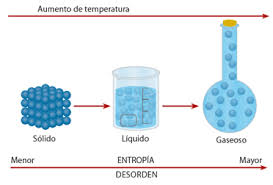
Función termodinámica que es una medida de la parte no utilizable de la energía contenida en un sistema o materia. Sirve para medir el grado de desorden dentro de un proceso y permite distinguir la energía útil, que es la que se convierte en su totalidad en trabajo, de la inútil, que se pierde en el medio ambiente
Constante de equilibrio:
Es la relación que se establece entre las concentraciones de reactivos y productos cuando se alcanza el estado de equilibrio

pH:
se trata de una unidad de medida de alcalinidad o acidez de una solución, mas específicamente el pH mide la cantidad de iones de hidrógeno que contiene una solución determinada, el significado de sus sigla son potencial de hidrogenaciones, el pH se ha convertido en una forma practica de manejar cifras de alcalinidad, en lugar de otros métodos un poco mas complicada.

poh:
El pOH (o potencial OH) es una medida de la acidez o alcalinidad de una disolución. También se emplea el pH = - log [H3O+] para medir la concentración de iones hidronio [H3O+]. Ejemplos de Cálculo del pOH: Ejemplo 1: calcular el pOH de una disolución 0,5 N de hidróxido de sodio NaOH.

Trabajos:
2-. calcular el Ce de cierta sustancia a la que se le aplica una cantidad de calor de 1221.39 Kj para que cambie su temperatura de 32.86 a 46.58 °C sabiendo que la masa de esa sustancia es de 2.57 Kg
Ce=Q/m(Ti-Tf) Ce=122139.0/2570.0*(32.52-46.58)
Ce=122139.0/2570.0(13.72)
Ce=122139.0/35260.4=34.63 J/g°C
3-.el lor especifico del Al es de 0.896 K/g°C ¿que cantidad de calor se requiere aplicar para contentar 45.7 g de Al para cambiar su temperatura de 29.8 a 36.9 °F
Q=m*Ce*Ti-Tf 29.8-32/1.8=1.2°C 36.9-32/1.8=-2.7°C 2.7+1.2=3.9
Q=45.7 g*0.896 J/g°C*3.9°C=159.69408 J
4-.¿cuantas calorías son necesarios para calentar 250 ml de agua para prepar café, si se calienta el agua de 18.9 a 62.8°C
Ce agua=4.184 J/g°C
Q=m*Ce*Ti-Tf Q=250g*1cal/g°C*43.9°C=10975.0 Cal
5-.En la combustión en el gas butano, se lobera una energia de -1065.3 Kj
a) calcular la entalpia que libera 57.3 g de etano?
b) calcular la entalpia del etano
2C2H+7O2-4Co2+6H2O
1.00797*6=6.04782 12.01115*2=24.02230
6.04782+24.02230=30.081 g/mol
57.30*1mol/30.08 g/mol=1.90
1065.3*1.90=2024.070
2/2024.070=1012.035 Kj
6-. H=(H°productos-reactivos)
H°=[(-397.7 Kj/mol)4]-[(-1065.3Kj/mol)]
H°=(-1590.8)-(-1065.3)
H°=-525.5 Kj/mol
7-. calorimetro
introducción:
Al mezclar dos cantidades de líquidos a distinta temperatura se genera una transferencia de energía en forma de calor desde el más caliente al más frío. Dicho tránsito de energía se mantiene hasta que se igualan las temperaturas, cuando se dice que ha alcanzado el equilibrio térmico. La cantidad de calor Q que se transfiere desde el líquido caliente, o la que absorbe el frío, responde a la expresión
materiales:
dos botes de alitro
bolitas de unicel
cinta maxqui
una lata
vascula
tubo de ensaye
hidrogeno de sodio
procedimiento:
primero pesar el acido y despues medir el agua de lo que queremos ocupar y mientras tanto debemos checar con que lo vamos amedir el agus y ya basier en acido en el bote de lata y asi poder ver a que temperatura llega la mescla
todos debemos checar como se encuentra las casas y tener mucho cuidado con las cosa que ocupemos y no tenr ninguna dificultad.
Q=m*Ce*Tf-Ti
Q=5.6*0.53*15°C
Q=29.400 cal
8-. Aluminio + Oxigeno _ Oxido de Aluminio
S°=396.7J/°k S°=422.6 J/°k S°=415.8 J/°K
Escribir la ecuación en formula
Al+O _ AlO
Balancear
4Al3+3O _ 2Al2O3
Calcular S°
S°r=831.6-2854.6=-2023.0
¿la reacción es espontanea o no?
no es espontanea porque nunca aumento entropia
9-. Accido poryodico+hidrogeno de calcio _ H2O+ yodo de calcio
H= 37.4 J/mol 42.7 J/mol 31.4 J/mol 28.6 J/mol
S°= 52.3 Kj/°K 25.6 Kj/°K 97.8 Kj/°K 30.5 Kj/°K
T= 20.5°C
Escribir formula
HIO+Ca(IOH) _ H2O+Ca(IO)
Baleanciar
2HIO4+Ca IOH2 _ 2H2O+Ca (IO4)2
Calcular H°
H°=(91.4 J/mol) - (117.5 J/mol)=-26.1 J/mol
Calcular S°
S°= 226100 J/°K - 130200 J/°K =-95900 J/°K
Calcular G°
G°=26.1 J/mol - 2816103500= 2816103661 J
10-. Acido nitroso + hidroxido cuprico _ Nitrito de cobre + oxido de hidrógeno
0.23 M 0.38 M 0.26 M 0.09 M
2HNO2+Cu(OH)2 _ Cu (NO)2+2H2O
Keq=[Cu(NO)2] [2H2O] / [2HNO2] [Cu(OH)2]=
Keq= 0.002106/0.020102= .104
11-. Calcular el pH y poh de una solucion de acido selenico que tiene una concentracion de 0.396 molar, considerando que el accido se lloniza al 100%
calcular la concentracion de iones hidroxilo de cierta sustancia de la que se sabe que su pH es de 9.7
pH= -Log(.792)= 0.1012
poh= 14-0.1012= 13.89
antilog-4.3
(OH)=5.01X10-5 mol/L.
12-."Para las personas que estan siguiendo una dieta alcalina es basico acerca del pH en sus cuerpos. pues de eso es lo que se trata la dieta, de balancear el nivel de pH para mantener un cuerpo alcalino y saludable. pero el conocimiento del nivel de pH no debe quedarse en lo basico. es recomendado conocer todo lo posible del pH para poder mantener la salud estable y el cuerpo alcalinos sin importar lo complicado que parezca.es por esto que interesado articulo habla de diferentes datos que se beben conocer acerca del pH"
Dr. Roberto O.
El pH nos sirve para indicar la concentracion de iones de hidrogenos que fluido en nuestro cuerpo donde ponemos darnos cuenta si tenemos nuestro pH muy alto o muy bajo, o tambien si esta bien equilibrado por medio de los alimentos que consumimos y asi no tengamos problemas con la salud y tambien no podamos engordar y tengamos nuestro peso bien establecido
" el equilibrio del pH se refiere a si tu cuerpo esta en un estado acido o alcalino. algunas personas tienen un equilibrio en el pH natural, por lo tanto, puedan estar libres de enfermedades. por otros lado, hay personas que tienen una tendencia a ser mas acidos y los alimentos que consumen les influyen especialmente de manera negativa en este aspectos y los provoca mayor acidificacion o ensuciamiento celular que otras. las enfermedades no pueden darse en un ambiente interior alcalino y oxigenado."
Gabriel Gavañino
todos los cuerpos tienen distintas reacciones en el cuerpo de pendiendo de los alimentos de los alimentos que consuma uno ya sean líquidos o comida, cada intenso lo aceptara y esa reaccion va hacer que los puedan decir si pude consumir acides fuertes o no lo puedan consumir, otras personas tienen mas cuidado con sus alimentos porque comen muchas cosas que esten elevados el pH, también hay que tener mucho cuidado porque si llega a elevarse el pH nos podemos enfermar por medio de la alientacion, también debemos cuidar y saber medirnos de nuestra salud es por nuestro bien para nadie mas solo nosotros como personas.
" el pH de la saliva es aproximadamente entre 6,5 y 7 esta compuesta de agua y de iones como el sodio, el cloro o el potasio, y enzima que ayudan a la desgracian inicial de los alimentos, cicatrices, protección contra infecciones bacterias e incluso funciones gustativas"
todos nosotros nos podemos quitar la sed con la saliva yes la principal de la con nos puede quitar la sed y también para poder obtener todo lo que tiene como unja forma de poder cuidar cada uno de los alimentos.
" Elp H es un baremo ideado para medir la alcalinidad o la acidez de una sustancia. ... El pH óptimo de lasangre humana debería ser ligeramente alcalino con un valor entre 7.35 y 7.45, pero por desgracia se estima que el 90% de los habitantes de los países supuestamente desarrollados sufren acidosis, incluyendo a los niños"
son todos lo que nos relacionamos como forma de poder entender como funcionan cada uno de los cuerpos de la manera como va circulando y asi poder observar las causa que tiene el cuerpo.
"En una persona sana el pH de la orina con un valor de 6,0 (rango normal de 4,5 a 8,0), es ligeramente ácido. Un valor de pH más alto (superior a 8) con presencia simultánea de nitrito, que normalmente no está presente en la orina, indica una infección bacteriana de las vías urinaria derivadas"
son cada uno como podemos cuidar nuestro curpo y tambien en nuestra forma de beber liquidos hay que cuidarnos como podemos sabe y no tener problemas con la salud
El jugo gástrico es una mezcla de secreciones de varias células epiteliales especializadas tanto superficiales como de lasglándulas gástricas. Su composición química consiste en agua, ácido clorhídrico, trazas de cloruro de potasio, cloruro de sodio, bicarbonato, enz
conclucion: todos somos capaces de poder reflecionar cada uno e los monetos mas complicados como podemos tener una idea y asi poder observar y no tener problemas y no tengamos problemas para nuestra salud y asi cuidarnos para no poder engordar con los conservadores de los alimentos
¿cual es el mejor trabajo que realizaste en este semestre?
el de Ce porque nos mustra a que esta la temperatura se encuentra las cosa y asi poder tener una idea y asi complicarnos la vida de poder adquirir algo
¿cual es el peor trabajo que realizaste en este semestre?
el de punto de equilibrio porque me costo por entender el tema y se complico en entender el tema
¿cual fue el tema que te parecio mas importante? explica
el mas importante es el de poh porque es coo el que nos va a seguir para poder cuidarnos y asi no tener un problema y checar nuestro acides de cada persona
¿cual fue el tema que te parecio menos importante?
fue el de Gibbs porque tiene menos importancia no tiene como se relaciona con la vida
explica como aplicas en tu vida diaria los conocimientos adquiridos en este curso
todos lo temas de este curso son como podemos tener una idea y no tengamos problemas con la vida y también con la formacion de cada uno de los temas de importancia de la vida.
a) ¿que se va hacer?
vamos a ver como podemos solucionar los problemas que tenemos y dar a conocer como se va a realizar
b) ¿como se va hacer?
se va a realizar por medios de unos ejercicios y poder solucionarlos
c) ¿para que se va hacer?
para poder demostrar cada uno de los temas que estuvimos realizando en este semestre
introducción:
Energía: la energia es la capacidad que posee los cuerpos para poder efectuar un trabajo a causa de su constitucion energia interna,de su posicion energia potencial o de su movimiento energia cinetica.es una magnitud homogenea con el gtrabajo po lo que se mide en las mismas unidades, es decir en julio en el sistemas internacional. segun la forma o el sistema fisico en que se manifiesta, se considera diferentes formas de energía: térmica, mecánica, eléctrica, química, electromagnético, nuclear, luminosa.
Entalpia:
es la cantidad de energia de un sistema termodinamica, que este puede intercambiar con su entorno
*es una reacion química a presión constante, rl cambio de entalpia del sistemos es el calor absorbido o desprendido en la reacion
Función termodinámica que es una medida de la parte no utilizable de la energía contenida en un sistema o materia. Sirve para medir el grado de desorden dentro de un proceso y permite distinguir la energía útil, que es la que se convierte en su totalidad en trabajo, de la inútil, que se pierde en el medio ambiente
Constante de equilibrio:
Es la relación que se establece entre las concentraciones de reactivos y productos cuando se alcanza el estado de equilibrio
pH:
se trata de una unidad de medida de alcalinidad o acidez de una solución, mas específicamente el pH mide la cantidad de iones de hidrógeno que contiene una solución determinada, el significado de sus sigla son potencial de hidrogenaciones, el pH se ha convertido en una forma practica de manejar cifras de alcalinidad, en lugar de otros métodos un poco mas complicada.
poh:
El pOH (o potencial OH) es una medida de la acidez o alcalinidad de una disolución. También se emplea el pH = - log [H3O+] para medir la concentración de iones hidronio [H3O+]. Ejemplos de Cálculo del pOH: Ejemplo 1: calcular el pOH de una disolución 0,5 N de hidróxido de sodio NaOH.
Trabajos:
2-. calcular el Ce de cierta sustancia a la que se le aplica una cantidad de calor de 1221.39 Kj para que cambie su temperatura de 32.86 a 46.58 °C sabiendo que la masa de esa sustancia es de 2.57 Kg
Ce=Q/m(Ti-Tf) Ce=122139.0/2570.0*(32.52-46.58)
Ce=122139.0/2570.0(13.72)
Ce=122139.0/35260.4=34.63 J/g°C
3-.el lor especifico del Al es de 0.896 K/g°C ¿que cantidad de calor se requiere aplicar para contentar 45.7 g de Al para cambiar su temperatura de 29.8 a 36.9 °F
Q=m*Ce*Ti-Tf 29.8-32/1.8=1.2°C 36.9-32/1.8=-2.7°C 2.7+1.2=3.9
Q=45.7 g*0.896 J/g°C*3.9°C=159.69408 J
4-.¿cuantas calorías son necesarios para calentar 250 ml de agua para prepar café, si se calienta el agua de 18.9 a 62.8°C
Ce agua=4.184 J/g°C
Q=m*Ce*Ti-Tf Q=250g*1cal/g°C*43.9°C=10975.0 Cal
5-.En la combustión en el gas butano, se lobera una energia de -1065.3 Kj
a) calcular la entalpia que libera 57.3 g de etano?
b) calcular la entalpia del etano
2C2H+7O2-4Co2+6H2O
1.00797*6=6.04782 12.01115*2=24.02230
6.04782+24.02230=30.081 g/mol
57.30*1mol/30.08 g/mol=1.90
1065.3*1.90=2024.070
2/2024.070=1012.035 Kj
6-. H=(H°productos-reactivos)
H°=[(-397.7 Kj/mol)4]-[(-1065.3Kj/mol)]
H°=(-1590.8)-(-1065.3)
H°=-525.5 Kj/mol
7-. calorimetro
introducción:
Al mezclar dos cantidades de líquidos a distinta temperatura se genera una transferencia de energía en forma de calor desde el más caliente al más frío. Dicho tránsito de energía se mantiene hasta que se igualan las temperaturas, cuando se dice que ha alcanzado el equilibrio térmico. La cantidad de calor Q que se transfiere desde el líquido caliente, o la que absorbe el frío, responde a la expresión
materiales:
dos botes de alitro
bolitas de unicel
cinta maxqui
una lata
vascula
tubo de ensaye
hidrogeno de sodio
procedimiento:
primero pesar el acido y despues medir el agua de lo que queremos ocupar y mientras tanto debemos checar con que lo vamos amedir el agus y ya basier en acido en el bote de lata y asi poder ver a que temperatura llega la mescla
todos debemos checar como se encuentra las casas y tener mucho cuidado con las cosa que ocupemos y no tenr ninguna dificultad.
Q=m*Ce*Tf-Ti
Q=5.6*0.53*15°C
Q=29.400 cal
8-. Aluminio + Oxigeno _ Oxido de Aluminio
S°=396.7J/°k S°=422.6 J/°k S°=415.8 J/°K
Escribir la ecuación en formula
Al+O _ AlO
Balancear
4Al3+3O _ 2Al2O3
Calcular S°
S°r=831.6-2854.6=-2023.0
¿la reacción es espontanea o no?
no es espontanea porque nunca aumento entropia
9-. Accido poryodico+hidrogeno de calcio _ H2O+ yodo de calcio
H= 37.4 J/mol 42.7 J/mol 31.4 J/mol 28.6 J/mol
S°= 52.3 Kj/°K 25.6 Kj/°K 97.8 Kj/°K 30.5 Kj/°K
T= 20.5°C
Escribir formula
HIO+Ca(IOH) _ H2O+Ca(IO)
Baleanciar
2HIO4+Ca IOH2 _ 2H2O+Ca (IO4)2
Calcular H°
H°=(91.4 J/mol) - (117.5 J/mol)=-26.1 J/mol
Calcular S°
S°= 226100 J/°K - 130200 J/°K =-95900 J/°K
Calcular G°
G°=26.1 J/mol - 2816103500= 2816103661 J
10-. Acido nitroso + hidroxido cuprico _ Nitrito de cobre + oxido de hidrógeno
0.23 M 0.38 M 0.26 M 0.09 M
2HNO2+Cu(OH)2 _ Cu (NO)2+2H2O
Keq=[Cu(NO)2] [2H2O] / [2HNO2] [Cu(OH)2]=
Keq= 0.002106/0.020102= .104
11-. Calcular el pH y poh de una solucion de acido selenico que tiene una concentracion de 0.396 molar, considerando que el accido se lloniza al 100%
calcular la concentracion de iones hidroxilo de cierta sustancia de la que se sabe que su pH es de 9.7
pH= -Log(.792)= 0.1012
poh= 14-0.1012= 13.89
antilog-4.3
(OH)=5.01X10-5 mol/L.
12-."Para las personas que estan siguiendo una dieta alcalina es basico acerca del pH en sus cuerpos. pues de eso es lo que se trata la dieta, de balancear el nivel de pH para mantener un cuerpo alcalino y saludable. pero el conocimiento del nivel de pH no debe quedarse en lo basico. es recomendado conocer todo lo posible del pH para poder mantener la salud estable y el cuerpo alcalinos sin importar lo complicado que parezca.es por esto que interesado articulo habla de diferentes datos que se beben conocer acerca del pH"
Dr. Roberto O.
El pH nos sirve para indicar la concentracion de iones de hidrogenos que fluido en nuestro cuerpo donde ponemos darnos cuenta si tenemos nuestro pH muy alto o muy bajo, o tambien si esta bien equilibrado por medio de los alimentos que consumimos y asi no tengamos problemas con la salud y tambien no podamos engordar y tengamos nuestro peso bien establecido
" el equilibrio del pH se refiere a si tu cuerpo esta en un estado acido o alcalino. algunas personas tienen un equilibrio en el pH natural, por lo tanto, puedan estar libres de enfermedades. por otros lado, hay personas que tienen una tendencia a ser mas acidos y los alimentos que consumen les influyen especialmente de manera negativa en este aspectos y los provoca mayor acidificacion o ensuciamiento celular que otras. las enfermedades no pueden darse en un ambiente interior alcalino y oxigenado."
Gabriel Gavañino
todos los cuerpos tienen distintas reacciones en el cuerpo de pendiendo de los alimentos de los alimentos que consuma uno ya sean líquidos o comida, cada intenso lo aceptara y esa reaccion va hacer que los puedan decir si pude consumir acides fuertes o no lo puedan consumir, otras personas tienen mas cuidado con sus alimentos porque comen muchas cosas que esten elevados el pH, también hay que tener mucho cuidado porque si llega a elevarse el pH nos podemos enfermar por medio de la alientacion, también debemos cuidar y saber medirnos de nuestra salud es por nuestro bien para nadie mas solo nosotros como personas.
" el pH de la saliva es aproximadamente entre 6,5 y 7 esta compuesta de agua y de iones como el sodio, el cloro o el potasio, y enzima que ayudan a la desgracian inicial de los alimentos, cicatrices, protección contra infecciones bacterias e incluso funciones gustativas"
todos nosotros nos podemos quitar la sed con la saliva yes la principal de la con nos puede quitar la sed y también para poder obtener todo lo que tiene como unja forma de poder cuidar cada uno de los alimentos.
" Elp H es un baremo ideado para medir la alcalinidad o la acidez de una sustancia. ... El pH óptimo de lasangre humana debería ser ligeramente alcalino con un valor entre 7.35 y 7.45, pero por desgracia se estima que el 90% de los habitantes de los países supuestamente desarrollados sufren acidosis, incluyendo a los niños"
son todos lo que nos relacionamos como forma de poder entender como funcionan cada uno de los cuerpos de la manera como va circulando y asi poder observar las causa que tiene el cuerpo.
"En una persona sana el pH de la orina con un valor de 6,0 (rango normal de 4,5 a 8,0), es ligeramente ácido. Un valor de pH más alto (superior a 8) con presencia simultánea de nitrito, que normalmente no está presente en la orina, indica una infección bacteriana de las vías urinaria derivadas"
son cada uno como podemos cuidar nuestro curpo y tambien en nuestra forma de beber liquidos hay que cuidarnos como podemos sabe y no tener problemas con la salud
El jugo gástrico es una mezcla de secreciones de varias células epiteliales especializadas tanto superficiales como de lasglándulas gástricas. Su composición química consiste en agua, ácido clorhídrico, trazas de cloruro de potasio, cloruro de sodio, bicarbonato, enz
conclucion: todos somos capaces de poder reflecionar cada uno e los monetos mas complicados como podemos tener una idea y asi poder observar y no tener problemas y no tengamos problemas para nuestra salud y asi cuidarnos para no poder engordar con los conservadores de los alimentos
¿cual es el mejor trabajo que realizaste en este semestre?
el de Ce porque nos mustra a que esta la temperatura se encuentra las cosa y asi poder tener una idea y asi complicarnos la vida de poder adquirir algo
¿cual es el peor trabajo que realizaste en este semestre?
el de punto de equilibrio porque me costo por entender el tema y se complico en entender el tema
¿cual fue el tema que te parecio mas importante? explica
el mas importante es el de poh porque es coo el que nos va a seguir para poder cuidarnos y asi no tener un problema y checar nuestro acides de cada persona
¿cual fue el tema que te parecio menos importante?
fue el de Gibbs porque tiene menos importancia no tiene como se relaciona con la vida
explica como aplicas en tu vida diaria los conocimientos adquiridos en este curso
todos lo temas de este curso son como podemos tener una idea y no tengamos problemas con la vida y también con la formacion de cada uno de los temas de importancia de la vida.
